Effort Estimation in Named Entity Tagging Tasks
Named Entity Recognition (NER) is an essential component of many Natural Language Processing pipelines but the process of creating training corpora for NER in new domains is expensive, considering both time and monetary costs (Marrero 2013). At DefinedCrowd, we circumvent this issue by collecting and enriching data at scale through crowdsourcing.
Nonetheless, managing these annotations at scale raise other issues such as the prediction of completion timelines and fair pricing estimation for workers in advance. To that end, in this blogpost we present how at DefinedCrowd we estimate the effort needed for a human to complete a Named Entity Tagging (NET) task before the actual annotation takes place. For a complete version of the investigation, refer to the published paper (Gomes, et al. 2020).
Named Entity Tagging in Crowdsourcing
Crowdsourcing can be used to annotate large quantities of data by assigning Human Intelligence Tasks (HITs) to an existing pool of non-expert contributors, that complete it within a short time, in exchange for a monetary reward (Hassan 2013). In NET instances, the contributor’s goal is to locate and annotate pre-defined named entities in unstructured text. Figure 1 shows an example where the contributor will iteratively highlight a segment of text with a named entity and select the corresponding category.
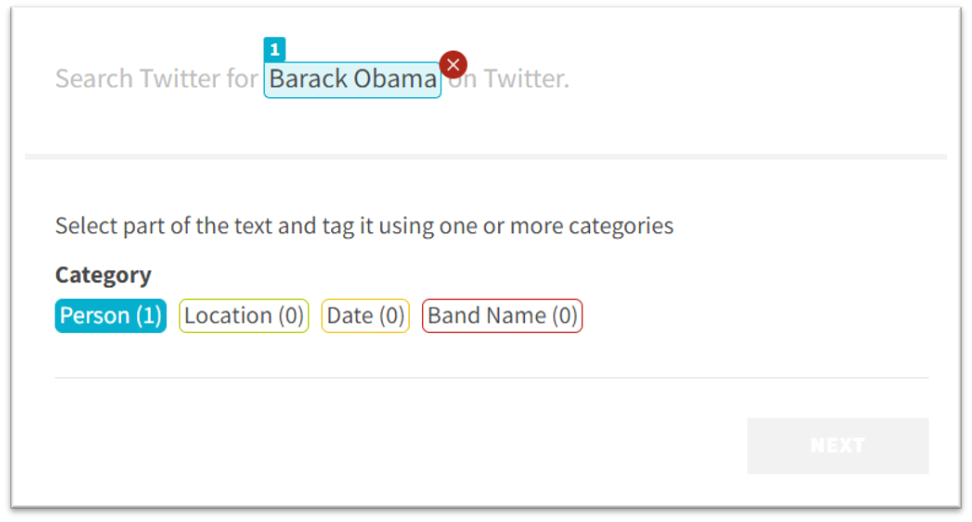
Figure 1: Example of a Named Entity Tagging HIT in Neevo
Human Effort Definition
Human effort represents the time needed by a human for completing a given HIT, that is, the interval since the HIT is shown and submitting it. For representability and comprehension purposes, we normalize time-on-task by the number of tokens present in the input. This transformation results in speed-on-task, which is measured in words per minute (wpm) and given by:
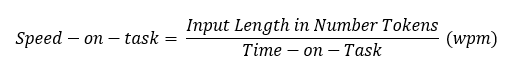
Considering that at DefinedCrowd NET data collection pipelines have a given redundancy, that is, each HIT is executed per more than one contributor, the average speed-on-task is our ultimate variable to predict.
Data Curation
When executing a HIT, external factors including contributor carelessness (such as leaving the HIT open for an unreasonable amount of time) or contributor expertise (where an experienced contributor completes tasks at a very fast pace) may impact the completion time. These undesirable data points are HITs that stand apart from the average speed-on-task (i.e. the target variable) behavior, so we must curate our dataset by discarding them.
For this, we investigate the speed-on-task’s standard deviation (SD) for each HIT: a value of zero represents perfect alignment, i.e., all contributors performed the task at the exact same speed (optimal condition); larger values for the standard deviation imply discrepant speeds and, therefore, are not good candidates to be used for training nor testing the prediction of human effort.
To make the process of data curation systematic, we use the concept of Inter-Annotator Agreement (IAA) applied to the speed-on-task values, measuring the Krippendorff’s alpha (𝛼) coefficient of the dataset (Krippendorff 1980). Our goal was to remove HIT executions with large speed-on-task, until the remaining dataset reached an agreement of 𝛼≥0.65 .
Figure 2 plots the tradeoffs between the value of IAA with respect to both number of HITs remaining in the dataset (on the left) and standard deviation of speed-on-task (on the right). We observe that the first setting where the ideal condition is met ( 𝛼≥0.65), corresponds to accepting HITs for which their speed-on-task standard deviation is below 20 wpm, resulting on a total dataset size of 37,061 HITs.
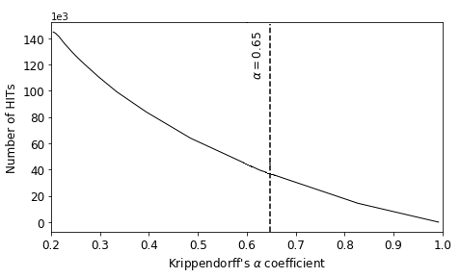
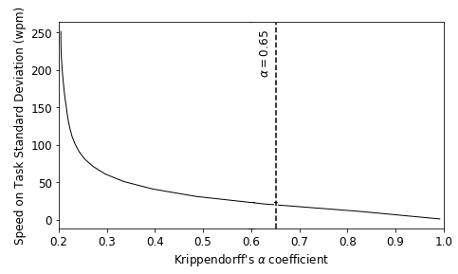
Figure 2: Kripendorff’s alpha and dataset size evolution given the allowed speed-on-task standard deviation threshold.
Predicting Human Effort
As a first approach to predict human effort, we establish a linear model baseline with two features. The features used represent the dimensions described in the literature review on the topic (Feyisetan 2015) (Sweller 1994): input length in number of tokens, as a basic representation of the amount of information to be processed, and number of categories of named entities, as a representation of cognitive load. Although we believe that the input length in number of tokens may evolve linearly with the effort needed to complete a task, we do not expect the taxonomy size to affect equally the annotation time. Thus, we explore the impact of using nonlinear approaches to the experiment. Then, we expand the set of explanatory variables adding text preprocessing features that can model the cognitive load associated with the task: number of sentences, number of punctuation tokens, number of stopwords and average word length (with and without stopwords).
Table 1 shows the experiments results. We conclude that the Nearest Neighbors Regressor outperforms the remaining models, attaining 25.68 wpm RMSE (Root Mean Squared Error), with a statistically significant improvement of 6%, when comparing to the linear model baseline. The final set of features used by the Nearest Neighbors are input length in number of tokens, number of categories of named entities, number of stopwords, number of punctuation tokens and average word length.
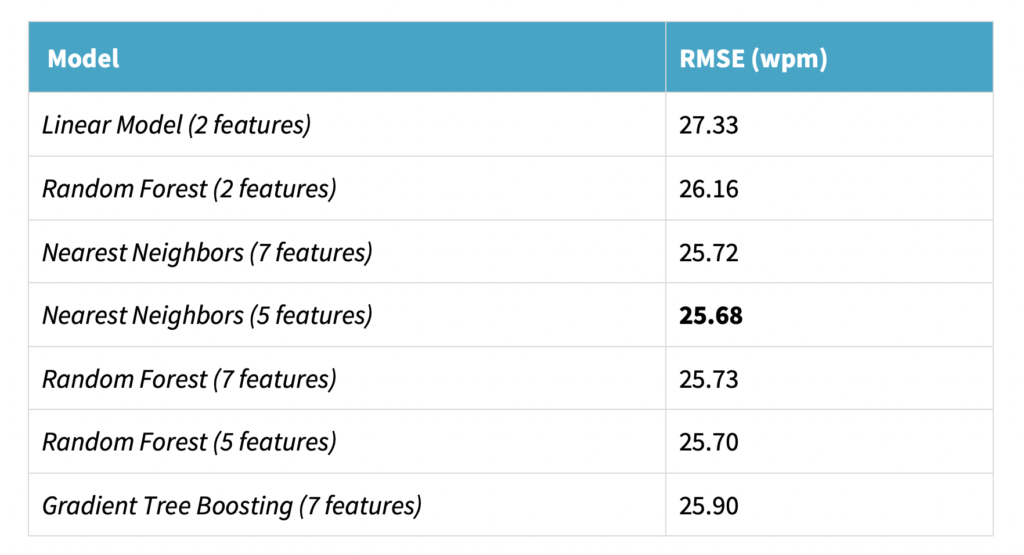
Table 1: Performance of predicting human effort using Nonlinear Models with the complete set of features (7), the reduced set of features for the Nearest Neighbors and Random Forest (5), compared with the Random Forest and Linear Model with a set of two features.
Interpreting the Human Effort Explanatory Variables
To understand the importance of each feature on the winning model, we decide to carry out an ablation study. Table 2 shows the rank of the features ordered by the highest impact on the model performance.
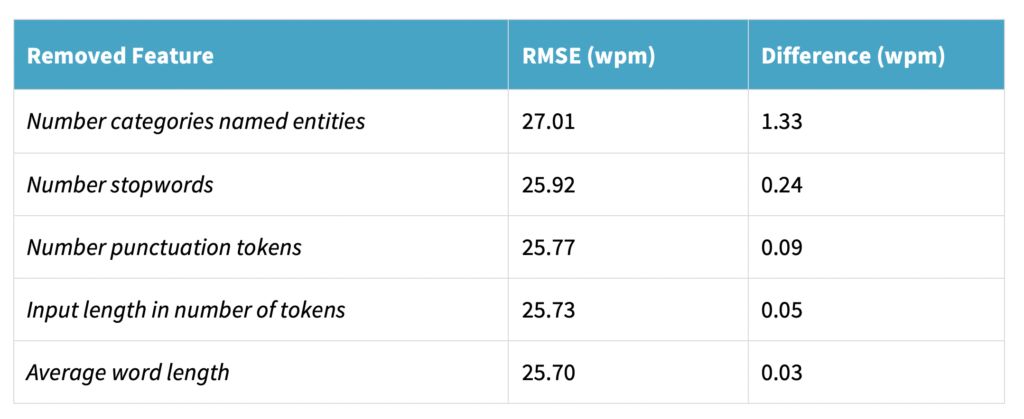
Table 2: RMSE obtained when removing each feature from the Nearest Neighbors model and the difference between the performance attained without each feature and the performance when using the set of five features (25.68 wpm).
That is to say that the number of categories of named entities is the feature with greater influence on the model performance. This feature is intuitively more relevant to explain the human effort, as the more entities to tag, the longer the task comprehension and the answering time. At the same time, the values for number of stopwords and the number of punctuation tokens prove that these features impact the speed-on-task, the former by lowering the cognitive effort and the latter by improving the sentence comprehension.
Shortage of Predictability Exploration
Considering the experiment results, we explore if poor effort predictions may relate to the shortage of the answering/reading times explainability due to uncertain factors before the annotation takes place. Our hypothesis is that the reading time depends on the contributor assigned, and the answering time depends on the number of instances of named entities.
Figure 3 shows the speed-on-task aggregated by the number of instances of named entities by means of an error plot. An instance corresponds to the tagging result, for example, in Figure 1 there is one instance, i.e., the annotation of “Barack Obama” with the named entity category “Person“. The plot shows the average speed-on-task (represented with a black circle) and the standard deviation (represented by the whiskers). We notice a decreasing trend on the mean speed-on-task when the number of instances of named entities increases. We expected this correlation as the number of instances influences the answering time, that in turn influence the speed-on-task. Nevertheless, we must take into consideration the high variance among the number of instances of named entities, that may be the consequence of other factors such as the contributor profile and the HIT cognitive load.
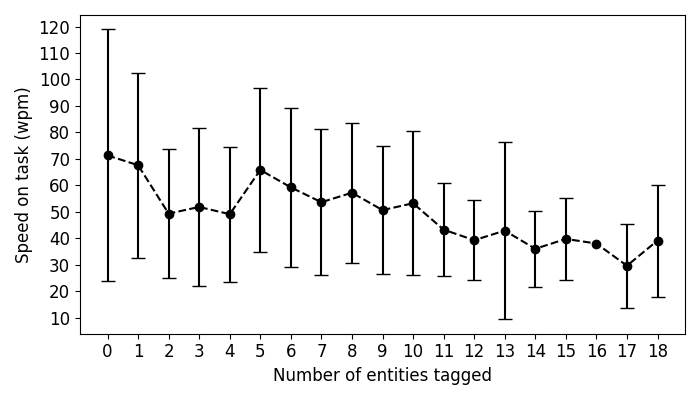
Figure 3: Mean and Standard Deviation of speed-on-task per number of instances of named entities.
Predicting Human Effort at the Job Level
By using the human effort at HIT level, we can estimate the total effort required by the crowd to complete a data collection pipeline. At DefinedCrowd we designate this pipeline as a job. Computing the job effort, i.e. the total human effort at the job level, is valuable as it provides insights that are useful for pricing and management.
To calculate it, we take into consideration the HITs available and the redundancy required for quality control. As we predict the human effort as the average speed-on-task (wpm), we must denormalize the results to estimate the job effort in hours. The following equation reflects the job effort estimation, where N is the number of HITs available in the job. Job Effort= ∑nN(InputLengthNumberTokensnPredictedSpeed−on−taskn∗Redundancy)
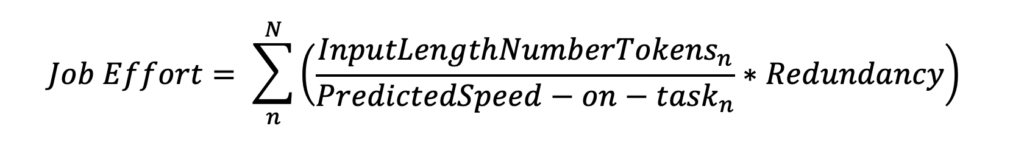
To verify the accuracy of our estimations, we compare the predicted job effort with our ground truth, that is, the sum of all HIT’s time-on-task. Figure 8 shows that our estimation is underpredicting. Considering that we employ the predicted efforts at the HIT level to compute the job effort, we deduce that these underpredictions are the result of overpredictions at the HIT level, corroborating the hypothesis that uncertain factors before the actual annotation takes place, affect the human effort predictability.
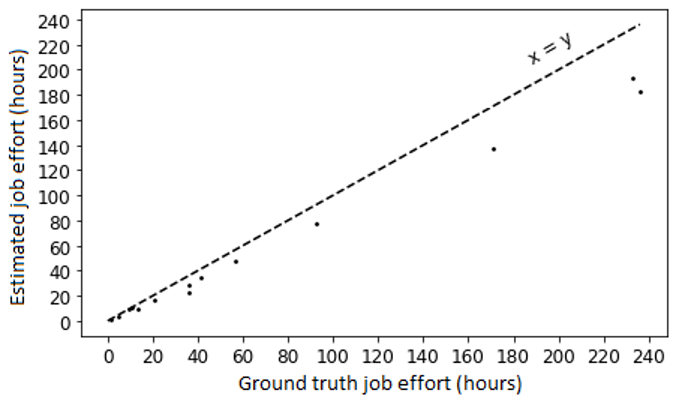
Figure 4: Estimated job effort in hours (y axis) as a function of the ground truth in hours. Each point in space represents one job. The x = y line is the identity line.
Finally, the job effort estimation achieved 18.10% MAPE (Mean Absolute Percentage Error). This was the first iteration and the results already allow us to establish thresholds for the human effort!
Bibliography
Feyisetan, Oluwaseyi and Luczak-Roesch, Markus and Simperl, Elena and Ramine, Tinati and Shadbolt, Nigel. 2015. “Towards Hybrid NER: A Study of Content and Crowdsourcing-Related Performance Factors.” Springer International Publishing Switzerland 2015 525-540.
Gomes, Inês, Rui Correia, Jorge Ribeiro, e João Freitas. 2020. “Effort Estimation in Named Entity Tagging Tasks.” Proceedings of the 12th Conference on Language Resources and Evaluation (LREC 2020). Marseille: European Language Resources Association (ELRA). 298-306.
Hassan, Umair ul and Curry, Edward. 2013. “A Capability Requirements Approach for Predicting Worker Performance in Crowdsourcing.” Proceedings of the 9th IEEE International Conference on Collaborative Computing: Networking, Applications and Worksharing 429-437.
Krippendorff, Klaus. 1980. “Reliability.” Em Content Analysis: An Introduction to Its Methodology, de Klaus Krippendorff, chapter 12. London: Sage.
Marrero, Mónica and Urbano, Julián and Sánchez-Cuadrado, Sonia and Morato, Jorge and Gómez-Berbís, Juan Miguel. 2013. “Named Entity Recognition: Fallacies, challenges and opportunities.” Computer Standards and Interfaces 482-489.
Sweller, John and Chandler, Paul. 1994. “Why some material is Difficult to Learn.” Cognition and Instruction 185-233.
